Lihatlah ECM atau wiring hardness sebuah mobil. Pada sebuah ECM, Anda akan menemukan bahwa satu sirkuit tersebut merupakan rangkainan berbagai komponen yang terintegrasi. Sementara pada wiring hardness, anda mungkin hanya akan menemukan satu kabel besar yang disambungkan ke (+) baterai, namun pada konektor yang terdapat pada kotak sekring anda akan menemukan puluhan terminal yang saling berhubungan. Itu artinya, dalam sebuah sistem kelistrikan kendaraan, akan ada ratusan rangkain pembagi tegangan.
1. Hukum Kirchhoff Arus dan Tegangan
Rangkaian listrik dibagi menjadi rangkaian seri, paralel dan seri/paralel tergantung dari cara penyambungannya. Dalam satu rangkaian, jumlah arus yang masuk dan arus yang keluar adalah sama, juga tegangan yang terpakai dengan tegangan yang turun adalah sama, inilah yang disebut dengan hukum Kirchhoff. Ada dua hukum Kirchhoff, Hukum Kirchhoff Arus (Kirchhoff Current Law, KCL) dan Hukum Kirchhoff Tegangan (Kirchhoff Voltage Law, KVL).
Hukum Kirchhoff Arus (hukum Kirchhoff pertama)
Dalam suatu rangkaian, jumlah aliran arus masuk dan jumlah aliran arus keluar adalah sama.

Sekarang, perhatikan Gambar berikut. Ada 5 cabang arus, dimana I1 dan I4 adalah arus masuk ke percabangan. Sementara I2, I3, dan I5 adalah arus yang keluar dari percabangan.
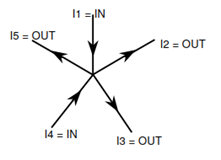
Dengan hukum Kirchhoff, arus pada percabangan diatas dapat ditulis sebagai berikut:
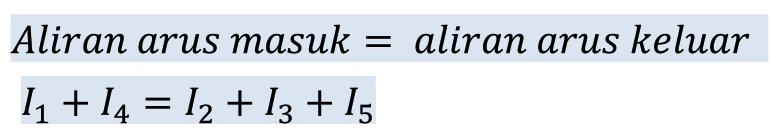
Hukum Kirchoff Tegangan (Hukum Kirchoff Kedua)
Tegangan sumber pada rangkaian seri sama dengan total masing-masing tegangan yang turun, jumlah penurunan tegangan dan tegangan yang dipakai adalah 0.

Mari kita lihat rangkaian sederhana dibawah ini.
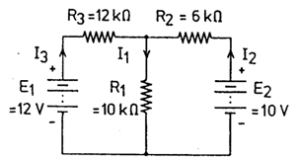
Dari contoh rangkaian pada gambar diatas, dengan hukum Kirchhoff dapat dituliskan beberapa persamaan matematis untuk menyatakan hukum Kirchhoff tegangan sesuai loop sebagai berikut.
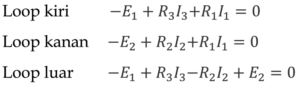
Semua komponen pada contoh gambar rangkaian diatas dilewati arus, sehingga sesuai hukum kirchhoff tegangan.
Pembuktian Hukum Kirchoof
Sekarang, mari kita lihat lagi rangkaian lain dibawah ini.
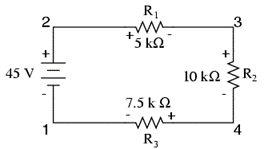
Jika kita menghubungkan voltmeter antara titik 2 dan 1, probe merah ke titik 2 dan probe hitam ke titik 1, voltmeter akan mencatat +45 Volt. Biasanya tanda (+) tidak ditampilkan. Namun, untuk pelajaran ini, polaritas pembacaan tegangan sangat penting dan kita akan menunjukkan angka positif secara eksplisit:
![]()
Bila tegangan ditentukan dengan subskrip ganda (karakter “2-1” pada notasi “E2-1”), itu berarti tegangan pada titik pertama (2) yang diukur mengacu pada titik kedua (1). Tegangan yang ditentukan sebagai “Ecd” berarti tegangan seperti yang ditunjukkan oleh voltmeter digital dengan probe merah pada titik “c” dan probe hitam pada titik “d”: Tegangan pada “c” mengacu pada “d” .
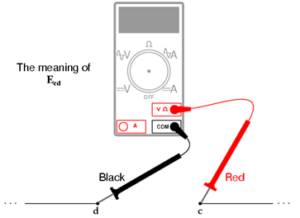
Gambar 1 Notasi polaritas
Kemudian, jika kita mengambil voltmeter yang sama dan mengukur penurunan tegangan pada masing-masing resistor (Gambar 2), mengelilingi sirkuit searah jarum jam dengan probe merah pada titik di depan dan probe hitam mengarah pada titik di belakang, kita akan mendapatkan bacaan berikut:
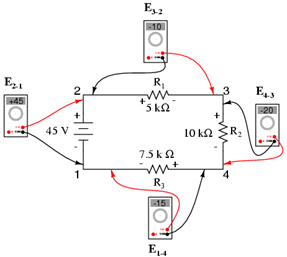
Gambar 2 Pengukuran tegangan dengan memperhatikan polaritas
Kita seharusnya sudah terbiasa dengan prinsip umum rangkaian seri yang menyatakan bahwa voltase drop pada setiap komponen sama dengan tegangan total. Mengukur voltage drop dengan cara seperti ditunjukkan pada Gambar 2 dan memperhatikan polaritas (tanda matematis) menunjukkan sisi lain dari hal ini.
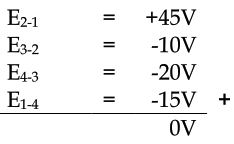
Ini mungkin lebih masuk akal jika kita menggambar ulang rangkaian pada Gambar 2, sehingga semua komponen terwakili dalam garis lurus.
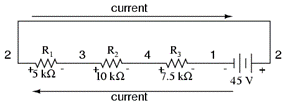
Gambar 3 Rangkaian resistor dan sumber tegangan secara seri
Rangkaian seri pada Gambar 3 masih sama dengan Gambar 2, hanya dengan komponen yang disusun dalam bentuk yang berbeda. Tegangan baterai negatif di sebelah kiri dan positif di sebelah kanan, sedangkan semua tegangan jatuh resistor berorientasi ke arah lain, positif di sebelah kiri dan negatif di sebelah kanan. Hal ini karena resistor menahan aliran elektron yang didorong oleh baterai. Dengan kata lain, “dorongan” yang diberikan oleh resistor terhadap aliran elektron harus berada pada arah yang berlawanan dengan sumber gaya gerak listrik.
Di sini, kita akan melihat voltmeter digital yang ditunjukkan di setiap komponen di sirkuit ini, probe hitam di sebelah kiri dan probe merah di sebelah kanan, seperti yang ditata secara horisontal sebagai berikut:
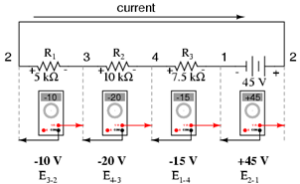
Gambar 4 Pengukuran voltage drop pada beban seri
Jika kita mengambil voltmeter yang sama dan membaca tegangan pada kombinasi komponen (Gambar 5), dimulai dengan hanya R1 di sebelah kiri dan maju melintasi keseluruhan rangkaian komponen (R1+R2, R1+R2+R3, R1+R2+R3+E1), kita akan melihat bagaimana tegangan menambahkan secara aljabar (ke 0):
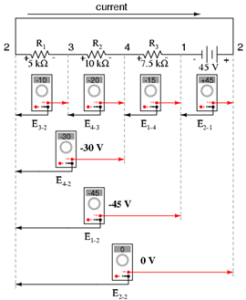
Gambar 5 Pembuktian hukum kirchhoff pada rangkaian seri
Hukum Kirchhoff Tegangan (KVL) juga akan bekerja untuk konfigurasi rangkaian paralel. Perhatikan bagaimana cara kerjanya untuk rangkaian paralel ini:
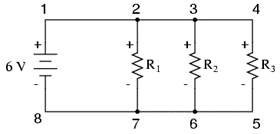
Gambar 6 Sirkuit pembagi arus
Dalam rangkaian paralel, tegangan pada setiap resistor sama dengan tegangan suplai. Dengan Gambar 6, tegangan yang disup0lai ke setiap resistor adalah 6 volt. Selanjutnya, tegangan pada loop 2-3-4-5-6-7-2 adalah:

Perhatikan tegangan akhir (sum) pada E2-2. Karena kita memulai urutan loop pada titik 2 dan berakhir pada titik 2, jumlah aljabar tegangan tersebut akan sama dengan tegangan yang diukur antara titik yang sama (E2-2), yang tentu saja harus nol.
Selanjutnya, “loop” yang kita telusuri untuk KVL tidak harus menjadi jalur arus nyata (sirkuit tertutup). Yang harus kita lakukan untuk mematuhi KVL adalah memulai dan mengakhiri pengukuran pada titik yang sama. Pertimbangkan contoh berikut, dengan menelusuri “loop” 2-3-6-3-2 di rangkaian resistor paralel yang sama (Gambar 6).

KVL dapat digunakan untuk menentukan tegangan yang tidak diketahui di sirkuit yang kompleks, di mana semua tegangan lain di sekitar “loop” tertentu diketahui. Ikuti rangkaian kompleks berikut ini (sebenarnya dua rangkaian rangkaian digabungkan dengan satu kawat di bagian bawah.
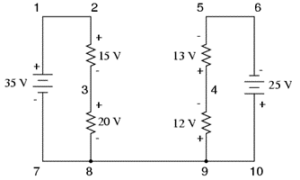
Gambar 7 Hukum kirchhoff pada rangkaian kompleks
Untuk membuat masalah lebih sederhana, nilai resistansi pada tiap tiap resistor dihilangkan dan hanya memberi nilai voltage drop pada setiap resistor. Dua rangkaian seri berbagi kawat di antara keduanya (kawat 7-8-9-10), membuat pengukuran tegangan mungkindilakukan antara dua rangkaian. Jika kita ingin menentukan tegangan antara titik 4 dan 3, kita bisa membuat persamaan KVL dengan tegangan antara titik-titik tersebut sebagai yang tidak diketahui.
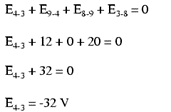
2. Konsep Rangkaian Seri
Sirkuit sederhana yang hanya memiliki beberapa komponen biasanya cukup mudah dimengerti oleh pemula. Namun demikian, pada rangkaian yang kompleks, analisisnya bisa menjadi lebih sulit karena melibatkan banyak percabangan, yang dirangkai secara seri dan paralel. Sebelum kita membahas detail tentang rangkaian seri, kita perlu menandai sebuah “simpul”. Simpul adalah persimpangan listrik antara dua komponen atau lebih. Bila rangkaian dimodelkan pada sebuah skema, simpulnya adalah kabel antar komponen tersebut.
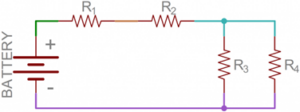
Gambar 8 Contoh skematis dengan empat simpul berwarna
Kita juga perlu memahami bagaimana arus mengalir melalui sebuah rangkaian. Arus mengalir dari tegangan tinggi ke tegangan rendah pada sebuah sirkuit. Sejumlah arus akan mengalir melalui setiap jalur yang bisa ditempuh untuk sampai ke titik tegangan terendah (biasanya disebut ground). Dengan menggunakan rangkaian di atas sebagai contoh, berikut adalah cara arus mengalir dari terminal positif baterai sampai ke terminal negatif.
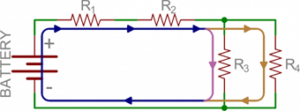
Gambar 9 Simpul arus
Perhatikan bahwa di beberapa simpul (seperti antara R1 dan R2) arusnya sama seperti pada saat keluar. Pada simpul lain (khususnya persimpangan tiga arah antara R2, R3, dan R4) arus utama (biru) terbagi menjadi dua yang berbeda. Itulah perbedaan utama antara seri dan paralel.
Dua komponen atau lebih dikatakan rangkaian secara seri jika mereka memiliki simpul yang sama dan jika arus yang sama mengalir melewatinya. Berikut adalah rangkaian contoh dengan tiga resistor seri.
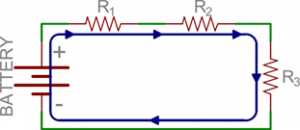
Gambar 10 Rangkaian seri
Dari Gambar 4.10, hanya ada satu jalur arus yang mengalir di sirkuit. Arus mengalir dari terminal positif baterai, kemudian akan melewati R1. Setelah keluar dari R1, arus akan mengalir langsung ke R2, lalu ke R3, dan akhirnya kembali ke terminal negatif baterai. Perhatikan bahwa hanya ada satu jalur untuk arus listrik. Inilah yang disebut rangkaian seri.
3. Konsep Rangkaian Paralel
Jika komponen berbagi dua simpul, maka keduanya adalah ragkaian paralel. Berikut adalah contoh skematik dari tiga resistor yang dirangkai paralel dengan baterai.
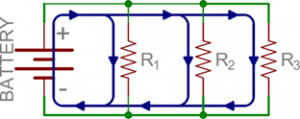
Gambar 11 Rangkaian paralel
Dari terminal baterai positif, arus mengalir ke R1, R2, dan R3. Simpul yang menghubungkan baterai ke R1 juga terhubung ke resistor lain. Ujung lain dari resistor ini juga saling terkait, lalu diikat kembali ke terminal negatif baterai. Ada tiga jalur arus listrik yang berbeda sebelum arus kembali ke baterai. Inilah yang disebut rangkaian paralel. Jika dalam rangkaian seri semua komponen (R) dilewati arus yang sama, rangkaian paralel memiliki tegangan yang sama untuk semua komponen (R).
4. Konsep Rangkaian Kombinasi
Kenyataannya, dalam sebuah sirkuit terpadu, komponen komponen listrik dirangkai secara seri dan pararel yang terintegrasi. Pada gambar berikut ini, kita kembali melihat tiga resistor dan baterai. Dari terminal baterai positif, arus mengalir ke R1. Setelah itu, simpul terpecah, dan arusnya menuju ke R2 dan ke R3. Setelah melalui R2 dan R3, simpulnya diikat kembali dan arus kembali ke terminal negatif baterai.
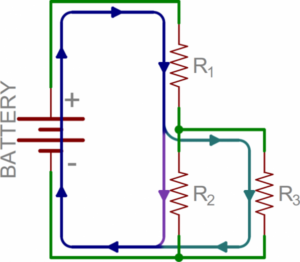
Gambar 12 Rangkaian kombinasi
5. Tahanan Equivalen pada Rangkaian Seri
Ketika kita menempatkan beberapa resistor dalam sebuah rangkaian, baik secara seri maupun paralel, kita telah mengubah cara arus mengalir melewatinya. Sebagai contoh, jika kita memiliki suplai 10V di resistor 10k, hukum Ohm mengatakan bahwa kita memiliki arus 1mA yang mengalir.
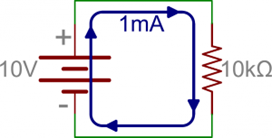
Gambar 13 Loop arus pada rangkaian
Jika kita kemudian menempatkan resistor 10kΩ lain secara seri dengan yang pertama dan menjaga tegangan sumber tetap 10V, arus akan turun menjadi 0,5 1mA karena resistansinya bertambah dua kali lipat.
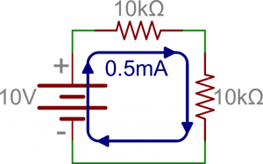
Gambar 14 Hukum Ohm pada rangkaian seri
Dengan kata lain, nilai resistansi pada rangkaian seri adalah penambahan dari semua nilai tahanan yang ada.
Latihan 1
Sebuah rangkain sederhana seperti ditunjukkan dalam gambar berikut. Hitung nilai tahanan equivalen, arus yang mengalir pada rangkaian, dan Voltage drop pada setiap resistor
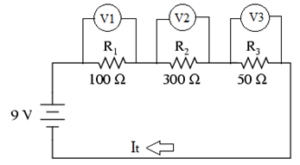

6. Tahanan Equivalen pada Rangkaian Paralel
Bagaimana dengan resistor yang dirangkai secara paralel? Pertimbangkan contoh terakhir di mana kita mulai dengan suplai 10V dan resistor 10kΩ (Gambar 4.13), tapi kali ini kita menambahkan 10kΩ lagi secara paralel, bukan seri. Sekarang ada dua jalur arus listrik. Karena tegangan suplai tidak berubah, Hukum Ohm mengatakan resistor pertama masih akan menarik arus 1mA dan begitu juga resistor kedua, dan sekarang kita memiliki total 2mA yang berasal dari Sumber tegangan 10V. Ini menyiratkan bahwa kita telah mengurangi total hambatan menjadi dua.

Gambar 15 Hukum Ohm pada rangkaian paralel
Persamaan untuk menambahkan sejumlah resistor yang dirangkai secara paralel adalah sebagai berikut.
![]()
Jika hanya ada dua resistor dapat disederhanakan menjadi
![]()
Latihan 2
Sebuah rangkain paralel seperti ditunjukkan dalam gambar berikut. Hitung nilai tahanan equivalen dan arus yang mengalir pada setiap beban.
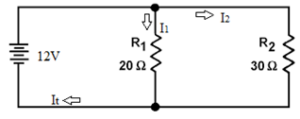
Penyelesaian:

Latihan 3
Sebuah rangkain kombinasi seri-paralel seperti ditunjukkan dalam gambar berikut. Hitung nilai tahanan equivalen, tegangan, dan arus yang mengalir pada setiap titik pengukuran.
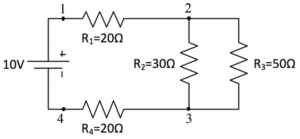
Penyelesaian

7. Rangkaian Kapasitor
Menggabungkan kapasitor sama seperti menggabungkan resistor, tetapi berlaku persamaan sebaliknya. Kapasitor terdiri dari dua pelat yang saling berdekatan dan fungsinya dasarnya adalah memegang sejumlah elektron. Semakin besar nilai kapasitansi, semakin banyak elektron yang bisa dipegangnya. Jika ukuran pelat dinaikkan, kapasitansi naik karena secara fisik lebih banyak ruang bagi elektron untuk mengendap. Dan jika pelat dipindahkan lebih jauh, kapasitansi turun, karena kekuatan medan listrik di antara mereka turun saat jaraknya bertambah. Misal, kita punya dua kapasitor 10μF yang dihubungkan secara seri.

Gambar 16 Rangkaian kapasitor seri
Ingat bahwa dalam rangkaian seri hanya ada satu jalur arus yang mengalir. Ini berarti bahwa jumlah elektron yang dikeluarkan dari tutup di bagian bawah adalah sama dengan yang keluar dari tutup di atas sehingga kapasitansi belum meningkat.
Dengan menempatkan kapasitor secara seri, kita telah secara efektif memasang pelat lebih jauh karena jarak antar pelat dari dua kapasitor ditambahkan secara bersamaan. Jadi kita tidak memiliki 20μF, atau bahkan 10μF, tetapi hanya 5μF. Ini berarti kita menambahkan nilai kapasitor seri dengan cara yang sama seperti menambahkan nilai resistor secara paralel.
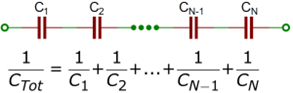
Gambar 17 Konsep penjumlahan nilai kapasitor seri
Tampaknya tidak ada gunanya menambahkan kapasitor secara seri. Tapi satu hal yang kita dapatkan adalah tegangannya naik dua kali lipat. Sama seperti baterai, saat kita memasang kapasitor secara seri, tegangan akan bertambah.
Menambahkan kapasitor secara paralel seperti menambahkan resistor secara seri, nilainya ditambahkan. Menempatkan kapasitor secara paralel, secara efektif akan meningkatkan ukuran pelat tanpa meningkatkan jarak di antara keduanya. Pelat yang lebih luas berarti kapasitansinya meningkat.
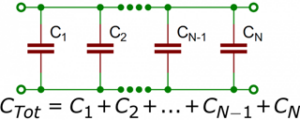
Gambar 20 Konsep penjumlahan nilai kapasitor paralel
Baca Juga:
- Teori Dasar Listrik
- Besaran Listrik
- Pengukuran Besaran Listrik
- Wheatstone bridge
- Elektromagnetik dan Aplikasinya
- Elektrokimia dan Aplikasinya
Referensi:
Setiyo, M. (2017) Listrik & Elektronika Dasar Otomotif (Basic Automotive Electricity and Electronics). Edited by A. Burhanudin. Magelang: UNIMMA Press.